利用FGSM攻击MNIST数据集(Pytorch)

发表于

前言

FGSM的全称是Fast Gradient Sign Method(快速梯度下降法），在白盒环境下，通过求出模型对输入的导数，然后用符号函数得到其具体的梯度方向，接着乘以一个步长，得到的“扰动”加在原来的输入 上就得到了在FGSM攻击下的样本。本文将实现在Pytorch框架下使用FGSM攻击MNIST数据集

训练模型的保存

通过之前MNIST识别的代码实现，我们就可以实现模型的保存。只需要在最后加上一行代码即可。

1
torch.save(model.state_dict(), "mnist_model.pth")

save函数有两个参数，第一个参数是模型的状态。其中model.state_dict()只保存模型权重参数，不保存模型结构，而model则保存整个模型的状态。这里我们使用model.state_dict()，第二个参数是路径和保存的文件名。这里我们保存在同级目录下，文件名是mnist_model.pth

训练模型完整代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
import torch
import torch.nn as nn
import torch.nn.functional as F
from torchvision import datasets,transforms
from torch.utils.data import DataLoader
import torch.optim as optim
batch_size = 16
epochs = 5
transforms = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.1307,),(0.3081,))
])

train_set = datasets.MNIST("data",train=True,download=True,transform=transforms)
test_set = datasets.MNIST("data",train=False,download=True,transform=transforms)


train_loader = DataLoader(train_set,batch_size=batch_size,shuffle=True)
test_loader = DataLoader(test_set,batch_size=batch_size,shuffle=True)

class Net(nn.Module):
    def __init__(self):
        super(Net,self).__init__()
        self.conv1 = nn.Conv2d(1,10,5)
        self.conv2 = nn.Conv2d(10,20,3)
        self.fc1 = nn.Linear(20*10*10,500)
        self.fc2 = nn.Linear(500,10)

    def forward(self,x):
        input_size = x.size(0) #获取batch_size
        x = self.conv1(x) #卷积
        x = F.relu(x) #激活
        x = F.max_pool2d(x,2,2) #池化
        x = self.conv2(x)
        x = F.relu(x)  # 激活
        x = x.view(input_size,-1) #拉平
        x = self.fc1(x)
        x = F.relu(x)
        x = self.fc2(x)
        output = F.log_softmax(x,dim=1)
        return output

model = Net()
optimizer = optim.Adam(model.parameters())

def train_model(model, train_loader,optimizer ,epoch):
    #模型训练
    model.train()
    for batch_index,(data,target) in enumerate(train_loader):
        #梯度初始化为0
        optimizer.zero_grad()
        #预测
        output = model(data)
        #计算损失
        loss = F.cross_entropy(output,target)
        #找到概率值最大的下标
        # pred = output.max(1,keepdim=True)
        #反向传播
        loss.backward()
        optimizer.step()
        if batch_index % 600 == 0:
            print("Train Epoch : {} \t Loss : {:.6f}".format(epoch,loss.item()))

def test_model(model,test_loader):
    #模型验证
    model.eval()
    #正确率
    correct = 0.0
    #测试损失
    test_loss = 0.0
    with torch.no_grad():#不会计算梯度也不会进行反向传播
        for data,target in test_loader:
            #测试数据
            output = model(data)
            #计算测试损失
            test_loss+=F.cross_entropy(output,target).item()
            #找到概率值最大的下标
            pred = output.max(1,keepdim=True)[1] #值 索引
            #pred = torch.max(output,dim=1)
            #pred = output.argmax(dim=1)
            #累计正确率
            correct += pred.eq(target.view_as(pred)).sum().item()
        test_loss /= len(test_loader.dataset)
        print("Test ---- Average loss : {:.4f},Accuracy : {:.3f}\n".format(test_loss,100.0*correct/len(test_loader.dataset)))

for epoch in range(1,epochs+1):
    train_model(model,train_loader,optimizer,epoch)
    test_model(model,test_loader)
torch.save(model.state_dict(), "mnist_model.pth")

攻击代码

相关模块的导入
1
2
3
4
5
6
7
import torch
import torch.nn as nn
import torch.nn.functional as F
from torchvision import datasets, transforms
import numpy as np
from torch.utils.data import DataLoader
import matplotlib.pyplot as plt

可能遇到的错误

1
2
OMP: Error #15: Initializing libomp.dylib, but found libiomp5.dylib already initialized.
OMP: Hint This means that multiple copies of the OpenMP runtime have been linked into the program. That is dangerous, since it can degrade performance or cause incorrect results. The best thing to do is to ensure that only a single OpenMP runtime is linked into the process, e.g. by avoiding static linking of the OpenMP runtime in any library. As an unsafe, unsupported, undocumented workaround you can set the environment variable KMP_DUPLICATE_LIB_OK=TRUE to allow the program to continue to execute, but that may cause crashes or silently produce incorrect results. For more information, please see http://openmp.llvm.org/

解决方法

1
2
import os
os.environ["KMP_DUPLICATE_LIB_OK"]="TRUE"
参数定义

其中epsilons是FGSM攻击所加的扰动，值不超过1。pretrained_model是预训练模型，也就是我们上面保存的训练模型。

1
2
epsilons = [0, .05, .1, .15, .2, .25, .3]
pretrained_model = "mnist_model.pth"
定义受攻击的模型

这里的模型与我们上面MNIST识别所定义的模型相同。我们使用两个卷积层和两个全连接层，具体定义如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Net(nn.Module):
    def __init__(self):
        super(Net,self).__init__()
        self.conv1 = nn.Conv2d(1,10,5)
        self.conv2 = nn.Conv2d(10,20,3)
        self.fc1 = nn.Linear(20*10*10,500)
        self.fc2 = nn.Linear(500,10)

    def forward(self,x):
        input_size = x.size(0) #获取batch_size
        x = self.conv1(x) #卷积
        x = F.relu(x) #激活
        x = F.max_pool2d(x,2,2) #池化
        x = self.conv2(x)
        x = F.relu(x)  # 激活
        x = x.view(input_size,-1) 
        x = self.fc1(x)
        x = F.relu(x)
        x = self.fc2(x)
        output = F.log_softmax(x,dim=1)
        return output
加载测试集
1
2
3
4
5
test_loader = DataLoader(
    datasets.MNIST('data', train=False, download=True, transform=transforms.Compose([
            transforms.ToTensor(),
            ])),
        batch_size=1, shuffle=True)
实例化模型
1
model = Net()
加载预训练模型
1
model.load_state_dict(torch.load(pretrained_model))
定义模型的评估模式

这里设置eval进行训练默认不开启Dropout和BatchNormalization

1
model.eval()
定义FGSM攻击模型

在FGSM攻击模型函数中一共有3个参数，第一个参数是原始图片，第二个参数是攻击的扰动量，一般在0～1之间，第三个参数是图像关于求导之后的损失。最后由于对抗样本可能会在（0，1）范围之外，所以通过clamp函数将加扰动之后的图片限制在（0，1）之间。

1
2
3
4
5
def fgsm_attack(image, epsilon, data_grad):
    sign_data_grad = data_grad.sign()
    perturbed_image = image + epsilon*sign_data_grad
    perturbed_image = torch.clamp(perturbed_image, 0, 1)
    return perturbed_image
定义测试函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
def test( model, test_loader, epsilon ):
    correct = 0
    adv_examples = []

    for data, target in test_loader:
        data.requires_grad = True #开启自动求导
        output = model(data)
        init_pred = output.max(1, keepdim=True)[1] #找到概率值最大的下标
        if init_pred.item() != target.item():
            continue

        loss = F.nll_loss(output, target) #计算损失
        model.zero_grad()
        loss.backward()

        data_grad = data.grad.data
        perturbed_data = fgsm_attack(data, epsilon, data_grad)

        output = model(perturbed_data) #对加扰后的图片进行重新分类

        final_pred = output.max(1, keepdim=True)[1] 
        if final_pred.item() == target.item():
            correct += 1
            #添加当epsilon为0的时候的5个对抗案例
            if (epsilon == 0) and (len(adv_examples) < 5):
                adv_ex = perturbed_data.squeeze().detach().cpu().numpy()
                adv_examples.append( (init_pred.item(), final_pred.item(), adv_ex))
        else:
            if len(adv_examples) < 5:
                adv_ex = perturbed_data.squeeze().detach().cpu().numpy()
                adv_examples.append( (init_pred.item(), final_pred.item(), adv_ex))

    final_acc = correct/float(len(test_loader))
    print("Epsilon: {}\tTest Accuracy = {} / {} = {}".format(epsilon, correct, len(test_loader), final_acc))

    # 返回最终准确率和对抗案例
    return final_acc, adv_examples
开始训练
1
2
3
4
5
6
7
8
accuracies = [] #记录准确率
examples = [] #记录对抗攻击实例

#针对每一个对抗扰动值进行一次训练
for eps in epsilons:
    acc, ex = test(model, test_loader, eps)
    accuracies.append(acc)
    examples.append(ex)
训练结果

1

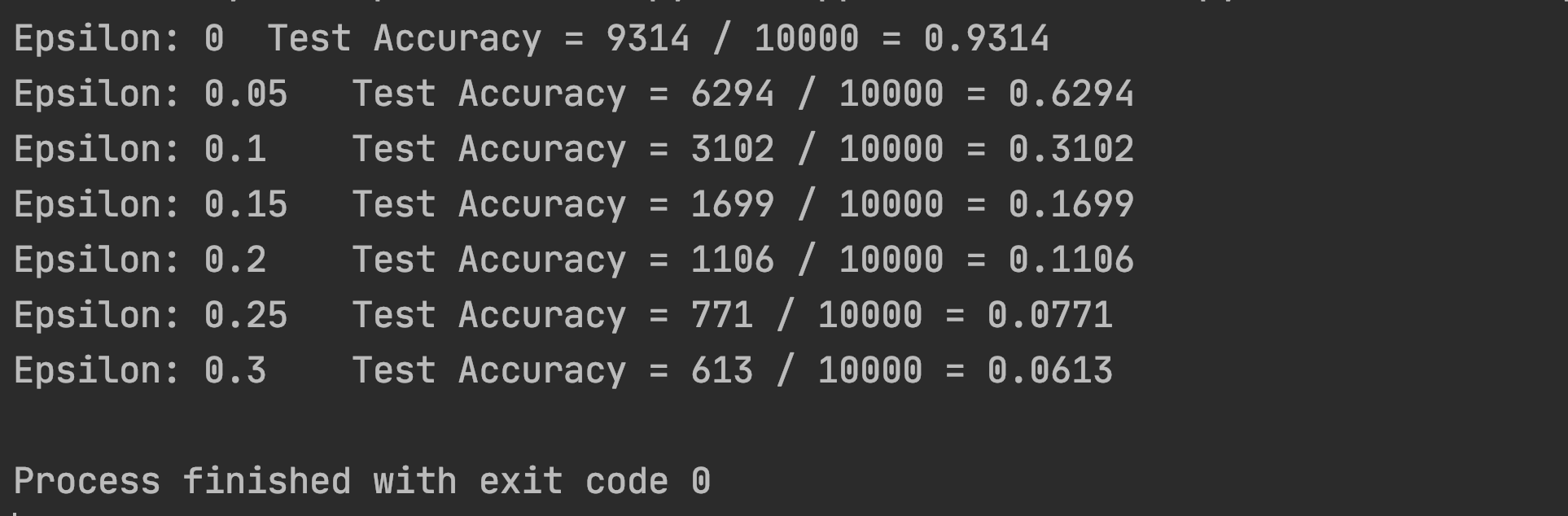
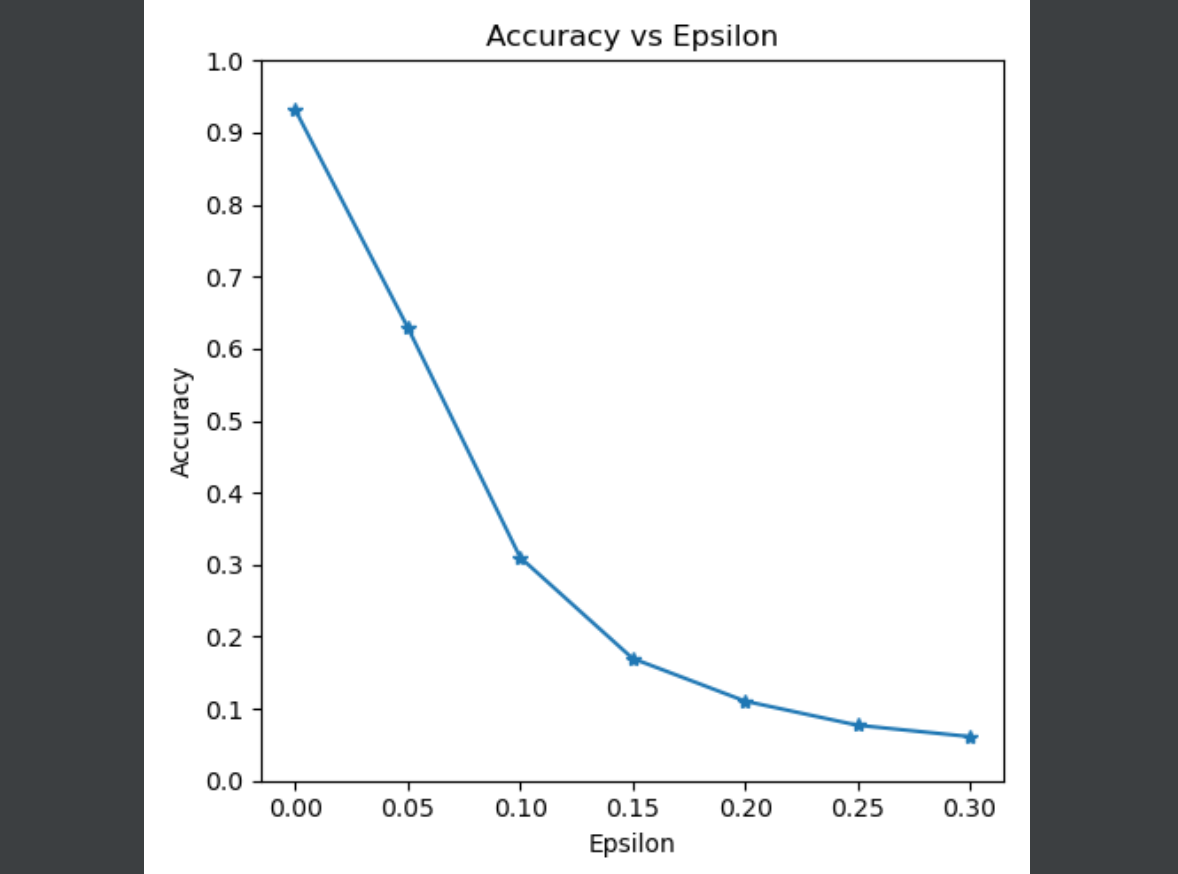
画出随着扰动值变化的准确率图

1
2
3
4
5
6
7
8
plt.figure(figsize=(5,5))
plt.plot(epsilons, accuracies, "*-")
plt.yticks(np.arange(0, 1.1, step=0.1))
plt.xticks(np.arange(0, .35, step=0.05))
plt.title("Accuracy vs Epsilon")
plt.xlabel("Epsilon")
plt.ylabel("Accuracy")
plt.show()

2

画出在不同扰动值下对抗实例图，每个扰动值对应5张照片。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
cnt = 0
plt.figure(figsize=(8,10))
for i in range(len(epsilons)):
    for j in range(len(examples[i])):
        cnt += 1
        plt.subplot(len(epsilons),len(examples[0]),cnt)
        plt.xticks([], [])
        plt.yticks([], [])
        if j == 0:
            plt.ylabel("Eps: {}".format(epsilons[i]), fontsize=14)
        orig,adv,ex = examples[i][j]
        plt.title("{} -> {}".format(orig, adv))
        plt.imshow(ex, cmap="gray")
plt.tight_layout()
plt.show()

3

FGSM攻击MNIST完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
import torch
import torch.nn as nn
import torch.nn.functional as F
from torchvision import datasets, transforms
import numpy as np
from torch.utils.data import DataLoader
import matplotlib.pyplot as plt

import os
os.environ["KMP_DUPLICATE_LIB_OK"]="TRUE"

epsilons = [0, .05, .1, .15, .2, .25, .3]
pretrained_model = "mnist_model.pth"

#CNN model defination
class Net(nn.Module):
    def __init__(self):
        super(Net,self).__init__()
        self.conv1 = nn.Conv2d(1,10,5)
        self.conv2 = nn.Conv2d(10,20,3)
        self.fc1 = nn.Linear(20*10*10,500)
        self.fc2 = nn.Linear(500,10)

    def forward(self,x):
        input_size = x.size(0) #获取batch_size
        x = self.conv1(x) #卷积
        x = F.relu(x) #激活
        x = F.max_pool2d(x,2,2) #池化
        x = self.conv2(x)
        x = F.relu(x)  # 激活
        x = x.view(input_size,-1) #拉平
        x = self.fc1(x)
        x = F.relu(x)
        x = self.fc2(x)
        output = F.log_softmax(x,dim=1)
        return output

test_loader = DataLoader(
    datasets.MNIST('data', train=False, download=True, transform=transforms.Compose([
            transforms.ToTensor(),
            ])),
        batch_size=1, shuffle=True)

model = Net()
model.load_state_dict(torch.load(pretrained_model))
model.eval()

# FGSM attack code
def fgsm_attack(image, epsilon, data_grad):
    sign_data_grad = data_grad.sign()
    perturbed_image = image + epsilon*sign_data_grad
    perturbed_image = torch.clamp(perturbed_image, 0, 1)
    return perturbed_image

def test( model, test_loader, epsilon ):
    correct = 0
    adv_examples = []

    for data, target in test_loader:
        data.requires_grad = True

        output = model(data)
        init_pred = output.max(1, keepdim=True)[1] 

        if init_pred.item() != target.item():
            continue

        loss = F.nll_loss(output, target)
        model.zero_grad()
        loss.backward()

        data_grad = data.grad.data
        perturbed_data = fgsm_attack(data, epsilon, data_grad)
        output = model(perturbed_data)

        final_pred = output.max(1, keepdim=True)[1] 
        if final_pred.item() == target.item():
            correct += 1
            if (epsilon == 0) and (len(adv_examples) < 5):
                adv_ex = perturbed_data.squeeze().detach().cpu().numpy()
                adv_examples.append( (init_pred.item(), final_pred.item(), adv_ex))
        else:
            if len(adv_examples) < 5:
                adv_ex = perturbed_data.squeeze().detach().cpu().numpy()
                adv_examples.append( (init_pred.item(), final_pred.item(), adv_ex))

    final_acc = correct/float(len(test_loader))
    print("Epsilon: {}\tTest Accuracy = {} / {} = {}".format(epsilon, correct, len(test_loader), final_acc))

    return final_acc, adv_examples

accuracies = []
examples = []

for eps in epsilons:
    acc, ex = test(model, test_loader, eps)
    accuracies.append(acc)
    examples.append(ex)

plt.figure(figsize=(5,5))
plt.plot(epsilons, accuracies, "*-")
plt.yticks(np.arange(0, 1.1, step=0.1))
plt.xticks(np.arange(0, .35, step=0.05))
plt.title("Accuracy vs Epsilon")
plt.xlabel("Epsilon")
plt.ylabel("Accuracy")
plt.show()

cnt = 0
plt.figure(figsize=(8,10))
for i in range(len(epsilons)):
    for j in range(len(examples[i])):
        cnt += 1
        plt.subplot(len(epsilons),len(examples[0]),cnt)
        plt.xticks([], [])
        plt.yticks([], [])
        if j == 0:
            plt.ylabel("Eps: {}".format(epsilons[i]), fontsize=14)
        orig,adv,ex = examples[i][j]
        plt.title("{} -> {}".format(orig, adv))
        plt.imshow(ex, cmap="gray")
plt.tight_layout()
plt.show()